Transformations

Transformations are fundamental tools for understanding and discussing geometry. This film examines dilations, one of the four basic types of transformations, and discusses how dilations are related to a machine called a pantograph.

Downloads

Transformations (140 Mb): Here you can download a copy of the film to watch offline.
Teaching Materials (PDF): Here you can download the worksheet that accompanies the materials. The download includes a key. A copy of the worksheet also appears below.
Pantograph Geogebra Demo: This link will take you to an excellent in-browser Geogebra demonstration (due to John Golden) in which you can interact with a digital pantograph.

Teaching Materials and Activities

Question 1

In the video, we saw how to dilate a shape using just a pencil and straight-edge. Use this technique to dilate the letter K below by a factor of 2. Use point c as your center point for the dilation.

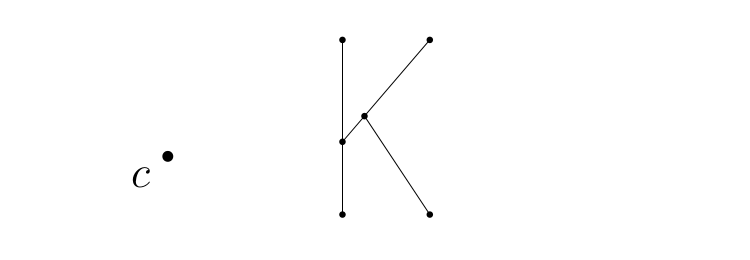
Question 2

In the video, we considered a pantograph that dilates shapes by a factor of 2. That machine had the following design:

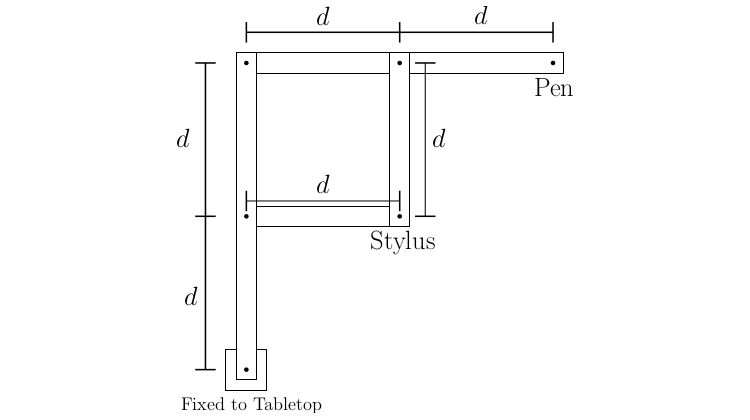
Part 1: How would you change the pantograph to dilate shapes by a factor of 1/2? Justify your answer geometrically.

Part 2: How would you change the pantograph to dilate shapes by a factor of 3? Justify your answer geometrically.

Question 3

Suppose an inventor presents you with the design for a drawing machine shown below. She claims that if you trace a shape with the stylus, the machine will draw a copy of the shape translated 10cm to the right. Explain why this machine performs a horizontal translation 10cm to the right.

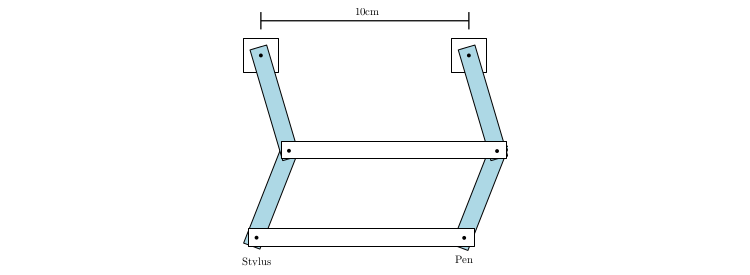
You should assume:

Dots represent hinges, and the two squares are fixed to the tabletop.
On each of the horizontal white bars, the distance between the hinge points is 10 cm.
The shaded bars are all of equal length.