Question 1

The Parallax Method is a technique for estimating distances that has applications in astronomy. The diagram below depicts our earth, the sun, and a distant star $A$. Suppose you want to estimate the distance between our Sun and the star $A$ marked in the picture.

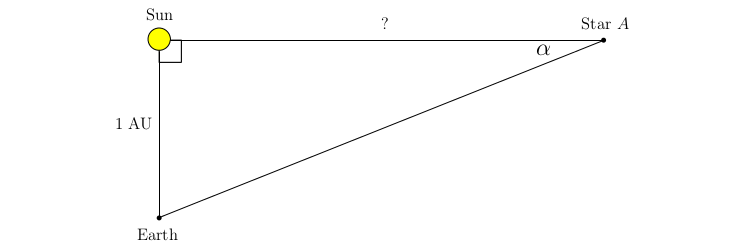
Part 1: Using your everyday knowledge of the solar system, discuss whether the diagram above is a scale model of the scenario we described. (You don't need to write down any formulas here, just think about how the distance from our earth to the sun compares with the distance from our sun to other stars.)

Part 2: Say you use a telescope to measure that angle $\alpha$ is $0.7611$ arcseconds (there are 3600 arcsecond in one degree) and the distance between earth and the sun is 1.000 astronomical unit (AU). Use trigonometry to determine the distance from the sun to star $A$ (in astronomical units). This is one of the main calculations astronomers perform when they use the parallax method!

Question 2

A pocket transit is a special type of compass that can be used for measuring angles.

As you can see, this tool consists of a compass, a mirror, and a sight. The sight allows you to align the compass with an object in your field of vision. Here's one way to hold the pocket transit:

This is what you would see if you were holding the transit and looking down at the compass:

Do you see the reflection of the sight in the mirror? By looking into the mirror, you can align the sight with an object (like a tree) while keeping the compass horizontally level. Then, by looking at the compass needle, you can measure the angle between that object and magnetic north.

Suppose you're standing at point $A$ on a North-South road, and in the distance you see a mountain.

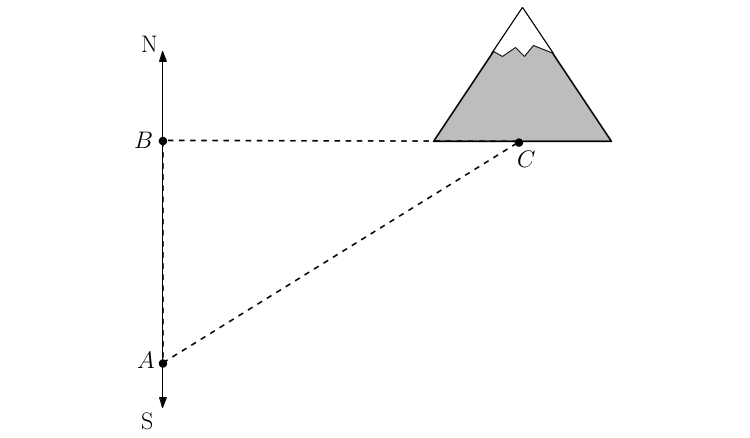
Using your pocket transit, you measure that at point $A$, the angle between point $C$ and due north is 67 degrees. Then, you drive in your car 100 km north along the road to point $B$. At point $B$, your pocket transit tells you the angle between point $C$ and due north is 90 degrees.

Part 1: Add the angles and lengths described in the story to the figure above.

Part 2: How far is point $B$ from point $C$? How far is point $A$ from point $C$?

Question 3

In the first part of the twentieth century, sailors (and many other people) used an instrument called a "Coincidence Rangefinder" to determine the distance between their boat and another object, such as another vessel or a light house. Here's one example of a coincidence rangefinder:

Here is another larger version:

The machine worked like this: The sailor would look through the eyepieces and see two different images, one for each of the two lenses on the machine. Here's an example of what a sailor might see before adjusting the instrument:

As you can see, the two images are slightly different!

By adjusting a knob, the sailor could move one of two images horizontally (by rotating a prism) until the images aligned. By examining how far the knob needed to be rotated, the sailor could estimate the distance to the object in question.

Below is a schematic of the important parts of a coincidence rangefinder that's being used to measure the distance to a tree:

Part 1: Do you see any important right triangles in this diagram? Indicate them by tracing their shape on the worksheet.

Part 2: Rotating the knob on the rangefinder rotates one of the prisms in the machine, which adjusts the view in one of the eyepieces. Suppose you've adjusted the knob so the views through the eyepieces match. What angle have you measured, in effect, by adjusting the knob? Indicate the angle on the diagram.

Part 3: Let's say the main prisms on the rangefinder are one meter apart and the important angle you measured in part 2 is called $\alpha$. Give a formula that would allow you to calculate the distance between the rangefinder and the tree, in terms of $\alpha$.